Introduction
Learning Map
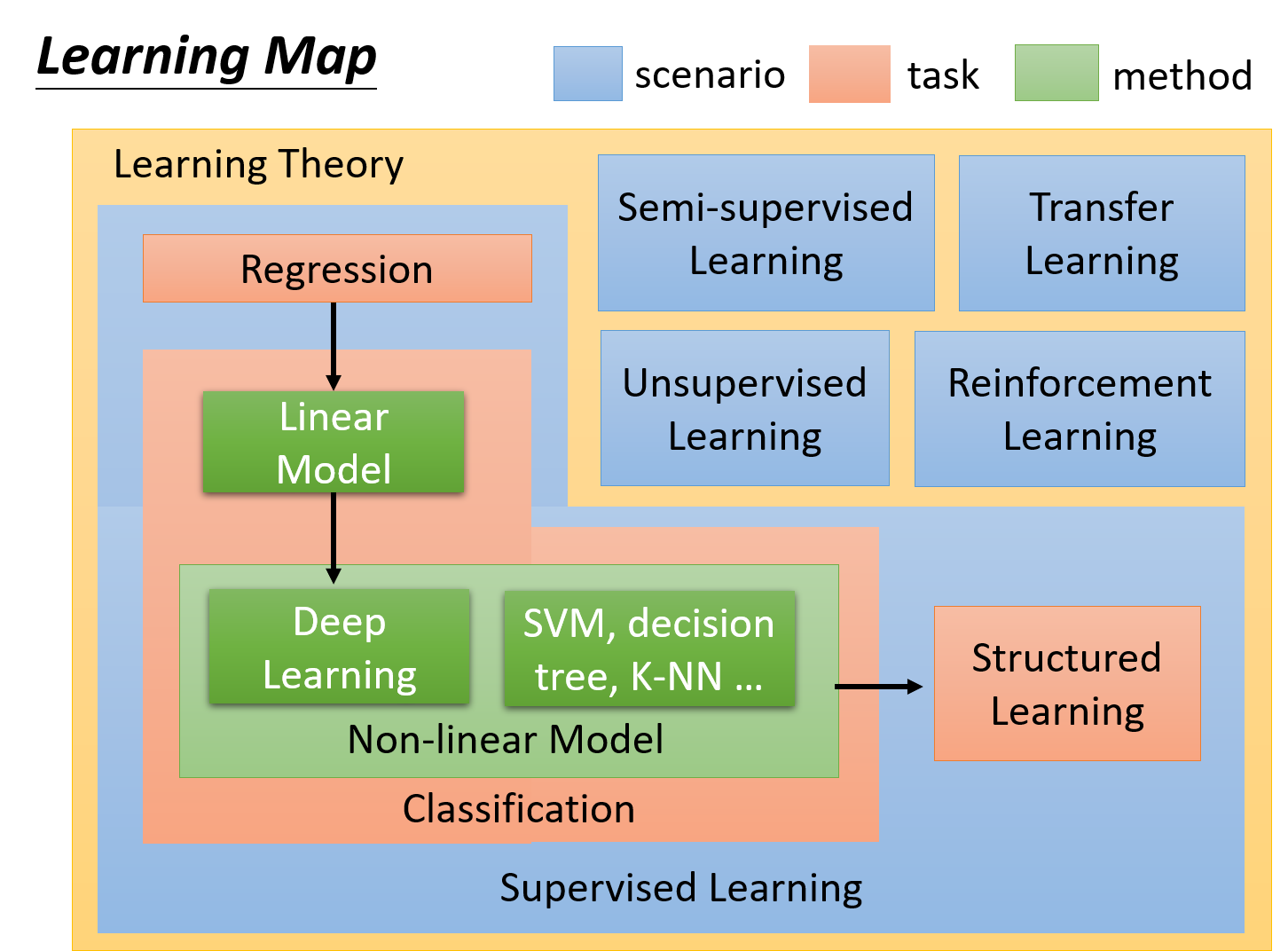
Supervised Learning(监督学习)
supervised learning 需要大量的training data,这些training data告诉我们说,一个我们要找的function,它的input和output之间有什么样的关系
而这种function的output,通常被叫做label(标签),也就是说,我们要使用supervised learning这样一种技术,我们需要告诉机器,function的input和output分别是什么,而这种output通常是通过人工的方式标注出来的,因此称为人工标注的label,它的缺点是需要大量的人工effort
Regression(回归)
regression是machine learning的一个task,特点是通过regression找到的function,它的输出是一个scalar数值
比如PM2.5的预测,给machine的training data是过去的PM2.5资料,而输出的是对未来PM2.5的预测数值,这就是一个典型的regression的问题
Classification(分类)
regression和classification的区别是,我们要机器输出的东西的类型是不一样的,在regression里机器输出的是scalar,而classification又分为两类:
Binary Classification(二元分类)
在binary classification里,我们要机器输出的是yes or no
Multi-class classification(多元分类)
在multi-class classification里,机器要做的是选择题,等于给他数个选项,每一个选项就是一个类别,它要从数个类别里面选择正确的类别
model(function set) 选择模型
- Linear Model(线性模型)
- Non-linear Model(非线性模型)
- deep learning
- SVM
- Decision Tree(决策树)
- KNN
Semi-supervised Learning(半监督学习)
数据只有少部分的labeled data,就是已经告诉这个数据的正确输出,但是还有大量的unlabeled data,比如区别猫和狗的样例,有一些labeled data(有注明该图片是猫还是狗),更多的是unlabeled data(只有图片)
Transfer Learning(迁移学习)
以区别猫和狗图片为例
我们也一样只有少量的有labeled的data;但是我们现在有大量的不相干的data(不是猫和狗的图片,而是一些其他不相干的图片),在这些大量的data里面,它可能有label也可能没有label
Transfer Learning要解决的问题是,这一堆不相干的data可以对结果带来什么样的帮助
Structured Learning(结构化学习)
在structured learning中,机器要输出一个有结构性的东西。在分类的问题中,机器输出的是一个选项,但是现实中往往是一些比较复杂的东西,简单的一维表示不了这么多东西,所以需要结构化的输出。
Reinforcement Learning(强化学习)
我们没有告诉机器正确的答案是什么,机器最终得到的只有一个分数,就是它做的好还是不好,但他不知道自己到底哪里做的不好,他也没有正确的答案;很像真实社会中的学习,你没有一个正确的答案,你只知道自己是做得好还是不好。其特点是Learning from critics
Regression Case Study
问题导入:预测宝可梦的CP值;已知宝可梦进化前的CP值,然后预测进化后的CP值
确定情景、任务、模型
我们有一些labeled data,即该宝可梦进化前的CP值和进化后的CP值。可以使用Supervised Learning
然后根据我们想要function的输出类型来确定Task,我们预期得到的是宝可梦进化后的cp值,是一个scalar,因此使用的Task是Regression
关于Model,选择很多,可以采用线性模型
设定具体参数
$X:$ 表示该样本,一只宝可梦
$X_{cp}:$ 进化前的CP值;$X_s$: 物种;$X_{hp}$:表示生命值;$X_w$:重量;$X_h$:高度;$f(X)$:目的函数;$y$:$y = f(X)$
模型
Liner Model
$$
y = w * X_{cp} + b
$$
扩充一下可以得到
$$
y = \sum_{i=0} ^ {n} w_i * x_i + b
$$
为了表示方便,$x_i^j$ 其中j表示第几只宝可梦,i表示宝可梦的第几个属性,$\widehat{y}$表示第i只的实际输出损失函数(Loss Function)
采用误差平方和形式表示
$$
L(f) = L(w,b) = \sum_{i=1}^n(\widehat{y}^i - (b + \sum_{i=0}^m w * x^j_i))^2
$$
我们需要确定$w$和$b$使得$L(f)$最小化,使用Gradient Descent梯度下降法

