人工智能学习笔记

第一讲人工智能概述

1.1 简介

1956年正式提出，被誉为20世纪三大科学技术成就（空间技术、原子能技术、人工智能技术）

1.2 人工智能的概念

对于智能到现在为止暂时没有一个准确的定义，只有一些主要流派。计算机人工智能暂时定义为智能是知识与智力的总和。

智能的特征：

1、感知能力（感知外部世界的能力，主要是视觉和听觉）

2、记忆与思维能力（存储与对于记忆信息的处理）

3、学习能力（分自主和无意识的学习）

4、行为能力（对于信息的输出）

1.3 人工智能的发展简史

提出(-1956年)->形成(1956-1969)->发展(1970-)

1.4 人工智能研究的基本内容不同学派

机器学习：监督学习、强化学习、非监督学习

符号主义：主要是面向逻辑符号的研究
连接主义：仿生应用（神经网络）
行为主义：感知-行动

计算智能定义

第二讲一阶谓词逻辑知识表示法

2.1 命题逻辑

$$
逻辑
\begin{cases}
经典逻辑(二值逻辑)
\begin{cases}
经典命题逻辑
\newline
一阶谓词逻辑
\end{cases}
\newline
非经典逻辑
\begin{cases}
三值逻辑
\newline
多值逻辑
\newline
模糊逻辑
\end{cases}
\end{cases}
$$

命题：一个非真即假的陈述句

2.2 谓词逻辑

谓词

一般形式：$P(X_1,X_2,…,X_N)$

个体$P(X_1,X_2,…,X_N)$：某个独立存在的事物或者某个抽象的概念。

谓词名$P$：刻画个体的性质、状态或个体间的关系。

个体是一个常量；一个或者一组指定的个体，一元谓词、二元谓词…

个体也可以是一个变量；此时真假可能不确定

个体还可以是函数；一个个体到另一个个体的映射

个体可以是谓词；二阶谓词等

谓词公式

非($\neg $)；或($\vee$)；与($\wedge$)；蕴含，表如果…那么…($\rightarrow $)；等价($\leftrightarrow$)

谓词逻辑真值表~~(或且非就不列了)~~

$P$	$Q$	$P \rightarrow Q$ （真假即假）	$P \leftrightarrow Q$ （相当于同或）
$T$	$T$	$T$	$T$
$T$	$F$	$F$	$F$
$F$	$T$	$T$	$F$
$F$	$F$	$T$	$T$

全称量词$\forall$；存在量词$\exists$

全称量词和存在量词的次序可能会影响命题的真假性

连接词的优先级从高到低($\neg \ >\ \wedge \ >\ \vee \ > \ \rightarrow \ > \ \leftrightarrow $)

量词的辖域：位于两次后面的单个谓词或者用括弧括起来的谓词公式（一般用全称量词和存在量词表示）

约束变量与自由变元：辖域内的变量就是约束变元，其他就是自由变元，但是这个是相对的。

谓词公式的性质

化简式：$P \wedge Q \Rightarrow P , P \wedge Q \Rightarrow Q$

附加式：$P \Rightarrow P \vee Q$

析取三段论：$\neg P , P \vee Q \Rightarrow Q$

假言推理：$P, P \rightarrow Q \Rightarrow Q$

拒取式推理：$\neg Q , P \rightarrow Q \Rightarrow \neg P$

假言三段论：$A \rightarrow B , B \rightarrow C \Rightarrow A \rightarrow C$

构造性二难：$P \vee Q , P \rightarrow R , Q \rightarrow R \Rightarrow R $

全称固化：$(\forall x)P(x) \Rightarrow P(y)$

存在固化：$(\exists x)P(x) \Rightarrow P(x_0)$

反证法：正难则反

2.3 一阶谓词逻辑知识表示法

一阶谓词逻辑知识表示法

1、定义谓词及个体

2、变元赋值

3、用连接词连接各个谓词，形成谓词公式

一阶谓词逻辑知识表示法特点

优点：自然性；精确性；严密性；容易实现

缺点：不能表示不确定的知识；组合爆炸；效率低

应用：自动问答系统；机器人行动规划系统；机器博弈系统；问题求解系统

第三讲产生式表示法和框架表示法

3.1 产生式表示法

IF P THEN Q 或者 P→Q

确定性规则知识产生式表示、不确定性规则知识产生式表示（加上置信度）、确定性事实性知识的产生式表示（三元组表示）、不确定性事实性知识的产生式表示（在前面的基础上机上置信度）

产生式与崔此逻辑中蕴含式的区别

1、产生式除了能表示蕴含，还可以表示操作规则、变换、函数等

2、蕴含只能表达精确的知识（非真即假），而产生式还能表示“可能”

巴克斯范式$BNF$：定义描述，$::=$表示定义为，$|$表示或，$[]$表示可缺省

graph TB
    A[控制] --> B[规则库]
    A --> C[推理机]
    A --> D[综合数据库]
    B --> C
    D --> C
    C --> D

规则库：用于描述相应领域内知识的产生式集合。

综合数据库（事实库、上下文、黑板等）：一个用于存放问题求解过程中各种当前信息的数据结构。

控制系统（推理机构）：由一组程序组成，负责整个产生式系统的运行，实现对问题的求解。

产生式优点：自然性、模块性、有效性、清晰性

缺点：效率不高、不能表达结构性知识

适用场合：1、领域知识间关系不密切，不存在结构关系。2、经验性及不确定性的知识，且相关领域中对这些知识没有严格、统一的理论。3、领域问题的求解过程可被表示为一系列相对独立的操作，且每个操作可被表示为一条或多条产生式规则。

3.2 语义网络表示法

语义基元

语义网络中最基本的语义单元称为语义基元，可用三元组表示为：
```
（结点1，弧，结点2）
```
基本网元
指一个语义基元对应的有向图，是语义网络中最基本的结构单元
实例关系： ISA
分类关系： AKO
成员关系： A-Member-of
上述关系的主要特征：属性的继承性，即处在具体层的结点可以继承抽象层结点的所有属性
属性关系：Have、Can
包含关系（聚类关系）：part-of
时间关系
位置关系
相近关系

可以有一对一关系，也可以有一对多和多对多的关系
优点：结构性、联想性、自然性
缺点：非严格性、复杂性

3.3 框架表示法

框架(frame)：一种描述所论对象属性的数据结构，一个框架由若干个“槽”的结构组成，每个槽又可根据实际情况分成若干个“侧面”。

槽(slot)：用于描述所论对象某一方面的属性

侧面(faced)：描述相应属性的某一方面（细分下的细分）

结构：

alt

特点：结构性、继承性、自然性、便于表达结构性的知识

第四讲基于谓词逻辑的推理方法

置换
- 可以简单理解维在一个谓词公式中用置换项去顶替变量
- 形如$\{ t_1 /x_1 ,t_2/x_2,…,t_n/x_n\}$
- 用$t_i$代替$x_i$
  - 使得$t_i$与$x_i$不相同
  - $x_i$不能循环出现在另一个$t_j$中（例如$\{ g(z)/x , f(x)/z \}$就不是一个置换，但是$\{ g(a)/x , f(x)/z \}$是置换，因为无循环递推）
- 设$\theta = \{ t_1 /x_1 ,t_2/x_2,…,t_n/x_n\}$，将$x_i$换成$t_i$得到$G$，称$G$为$F$在置换$\theta$下的例示，记作$G = F \theta$
- $\theta \circ \lambda$：$\theta = \{ t_1 /x_1 ,t_2/x_2,…,t_n/x_n\} \lambda= \{ u_1 /y_1 ,u_2/y_2,…,u_m/y_m\}$
  
  得到 $\{ t_1 \lambda /x_1 ,t_2 \lambda /x_2,…,t_n \lambda /x_n ,u_1 /y_1 ,u_2/y_2,…,u_m/y_m\}$。删除两种元素，一种为$t_i \lambda = x_i$；另一种为$y_j = x_i$
  - 其中值得注意的是$t_i \lambda$：用$\lambda$置换$t_i$，例如$f(y)/x$，$b/y$，置换成$f(b/y)/x = f(b)/x$
合一：设有公式集$F = \{F_1,F_1,…,F_n \}$，寻找一个置换$\theta$使得$F_1 \theta = F_2 \theta = … =F_n \theta$

归结演绎推理

反证法：$P \Rightarrow Q$，当且仅当$P \wedge \neg Q \Leftrightarrow F$，即$Q$为$P$的逻辑结论，当且仅当$P \wedge \neg Q$为假。

谓词公式转变为子句集

原子(atom)谓词公式：一个不能再分解的命题

文字：原子谓词公式及其否定

$P$：正文字；$\neg P$：负文字

子句：任何文字的析取式。任何文字本身也都是子句

空子句：不包含任何文字的子句，空子句是永假的

$A \rightarrow B$可化为$A \wedge \neg B$

$A \leftrightarrow B$可化为$( A \wedge B ) \vee ( \neg A \wedge \neg B )$

德摩根律（略）

化为Skolem标准型

化为前束形：前束形=(前缀){母式}，把量词约束提前

消去存在量词

存在量词不出现在全称量词的辖域内；存在量词出现在一个或者多个全称量词的辖域内。

Skolem化：用Skolem函数代替存在变量

$( \forall x_1)(( \forall x_2)…( \forall x_n)( \exists y)P(x_1,x_2,…,x_n,y)))$，存在量词$y$的Skolem函数为$y=f(x_1,x_2,…,x_n)$

Skolem标准型（分配律）

$P \vee (Q \wedge R) \Leftrightarrow (P \vee Q) \wedge (P \vee R)$

$P \wedge (Q \vee R) \Leftrightarrow (P \wedge Q) \vee (P \wedge R)$

略去全称量词

消去合取词：将上面的母式划分为若干个子句

子句变量标准化（每个子句变量不同）

谓词公式和子句集是否等价？

答：谓词公式和子句集不总是等价的，在谓词公式不可满足的条件下等价。在基于谓词逻辑的推理中，特别是归结推理中，把谓词公式转化为子句集是必要的。

鲁宾逊归结原理

子句集中子句之间都必须是合取关系

基本思想：首先检查$S$是否含空语句，若含则$S$不满足，否则去找子句进行归结，一旦出现空子句，那么$S$不满足。将互补的文字消去，留下的文字进行析取

归结：$C_1 ( \neg Q \vee P ), C_2 ( Q \vee R ) $可以化成$C_{12} ( P \vee R ) $

如果$C_1,C_2$为真，则$C_{12}$为真

若将$C_{12}$替换$C_1,C_2$得到$S_1$，与原来的$S_0$比较，$S_1$的不可满足性$\Rightarrow$ $S_0$的不可满足性

若将$C_{12}$加入$S_0$得到$S_2$，则$S_2$的不可满足性$\Leftrightarrow$ $S_0$的不可满足性

$C_1 = P(x) \vee Q(a),C_2 = \neg P(b) \vee R(x)$

令$C_2 =\neg P(b) \vee R(y)$，不同子句变量标准化

$L_1 = P(x),L_2=\neg P(b)$，则$\sigma = $ { $ b/x $ }

$C_{12} = Q(a) \vee R(y)$

值得注意的是，当归结的$P(x)$是两个变量，如$P(x) \vee R(x)$和$\neg P(y) \vee Q(y)$或者$P(x) \vee R(x)$和$\neg P(x) \vee Q(x)$都不能进行归结。

子句集$S$是不可满足的，当且仅当存在一个从$S$到空子句的归结过程
设$C_1$和$C_2$是两个没有公共变元的子句，$L_1$和$L_2$分别是$C_1$和$C_2$中的文字，如果$L_1$和$L_2$存在一个合一$\sigma$则：

$C_{12} = ( \{ C_1 , \sigma \} - \{ L_1 , \sigma \}) \cup ( \{ C_1 , \sigma \} - \{ L_1 , \sigma \}) $

归结反演

用$F$证明$Q$，我们构造集合$S = $ { $ F , \neg Q $ }，利用归结原理，将每次得到的归结式并入$S$中，若出现空语句则可停止，此时就证明了$Q$为真。

应用归结原理求解问题

用$F$求解$Q$，将$Q$用谓词公式表示，否定$Q$与answer构成析取式，加入$S$，此时$S = $ { $ F, \neg Q \vee ANSWER $ }，再通过归结，得到$ANSWER$，那么就能得出答案。

第五讲可信度方法和证据理论

部分内容

5.2 可信度方法

知识不确定性的表示

$IF \ \ \ \ E \ \ \ \ THEN \ \ \ \ H \ \ \ \ (CF(H,E))$；$CF(H,E)$：可信度因子，反映前提条件与结论的联系强度；取值范围：$[ -1 , 1 ]$

若$CF(H,E) > 0$，真的越确定；$< 0$，假的越确定；$= 0$，证据的出现与$H$无关

多个单一证据的合取：

$E = E_1 \ AND \ E_2 \ AND … AND \ E_n$，则$CF(E) = min(CF(E_1),CF(E_2),…,CF(E_n))$

多个单一证据的析取：

$E = E_1 \ OR \ E_2 \ OR … OR \ E_n$，则$CF(E) = max(CF(E_1),CF(E_2),…,CF(E_n))$

不确定的传递

$CF(H) = CF(H,E) \times max(0,CF(E))$

不确定的合成

$CF(H,E_1) , CF(H,E_2)$

$CF_1(H) = CF(H,E_1) \times max(0,CF(E_1))$

$CF_2(H) = CF(H,E_2) \times max(0,CF(E_2))$
$$
CF_{1,2}(H) =
\begin{cases}
CF_1(H)+CF_2(H)-CF_1(H)_2CF(H) & \text 若CF_1(H) \geq 0 , CF_2(H) \geq 0 \newline
CF_1(H) + CF_2(H) + CF_1(H)_2CF(H) & \text 若CF_1(H) < 0 , CF_2(H) < 0 \newline
\frac{CF_1(H)+CF_2(H)}{1-min ( | CF_1(H) | , | CF_2(H) | ) } & \text CF_1(H),CF_2(H) 异号
\end{cases}
$$

5.3 证据理论

概率分配函数

在证据理论中，$D$的任何一个子集$A$都对应一个关于$x$的命题，称该命题为“$x$的值是在$A$中”

特别的$M( \varnothing ) = 0 , \sum_{B \subseteq A} = 1$

概率分配函数是人工智能理论中非经典推理部分,证据理论中用到的一个函数，而概率是随机事件出现的可能性度量。

信任函数（下限函数）

$Bel \ : \ 2^D \rightarrow [0,1] ($对于任何一个属于$D$的子集$A$,命它对应一个数$M \in [0,1])$且$ Bel(A) = \sum_{B \subseteq A}^{} M(B) \ \ \ \ \forall A \subseteq D$

$Bel(A)$：对命题$A$为真的总的信任程度

$Bel(\varnothing) = M(\varnothing) = 0$

$Bel(D) = \sum_{B \subseteq D} M(B) = 1$

似然函数（上限函数）

又称不可驳斥函数或上限函数

$Pl(A) = 1 - Bel(\neg A)$

概率分配函数的正交和

设$M_1$和$M_2$是两个概率分配函数；则其正交和$M=M_1 \oplus M_2 : M(\varnothing) = 0$

$M(A) = K^{-1} \sum_{x \cap y = \varnothing} M_1(x) M_2(y)$

$K = 1 - \sum_{x \cap y = \varnothing }M_1(x) M_2(y) = \sum_{x \cap y \neq \varnothing } M_1(x) M_2(y)$

如果$K \neq 0$，则正交和$M$也是一个概率分配函数

如果$K = 0$，则不存在正交和$M$，即没有可能存在的概率函数，称$M_1$与$M_2$矛盾

特殊的概率分配函数

课本上着重讲的是这种概率分配函数，上文的概率分配函数都是一般的概率分配函数

特殊概率分配函数具有以下性质

为一般概率分配函数
$m(\{ s_i\}) \geq 0$
$\sum_{i=1}^{n} m (\{ s_i \}) \leq 1$
$m(\Omega) = 1 - \sum_{i=1}^{n} m (\{ s_i \})$
当子集个数等于1时，概率分配函数才有可能大于0，当子集中的元素大于1且不等于全集$\Omega$时，概率分配函数等于0
合成
- $$
  m(\{ s_i \}) = \frac{1}{K} [m_1(\{ s_i \}) m_2(\{ s_i \}) + m_1(\{ s_i \}) m_2(\Omega) + m_1(\Omega) m_2(\{ s_i \}) ]
  \\
  K = m_1(\Omega) m_2(\Omega) + \sum_{i=1}^{n}[m_1(\{ s_i \}) m_2(\{ s_i \}) + m_1(\{ s_i \}) m_2(\Omega) + m_1(\Omega) m_2(\{ s_i \}) ]
  $$
- $Bel(A) = \sum_{s_i \in A} m(\{ s_i \})$
- $Bel(\Omega) = \sum_{i=1}^n m(\{ s_i \}) + m(\Omega)$
- $Pl(A) = m(\Omega) + Bel(A)$

类概率概率函数
$$
f(A) = Bel(A) + \frac{|A|}{|\Omega|} \times [Pl(A) - Bel(A)]
$$

$f(\Omega) = 1 \ f(\varnothing)=0$
$Bel(A) \leq f(A) \leq Pl(A)$
$f(\neg A) = 1 - f(A)$

$H$的确定性$CER(H)$

MD(匹配程度)：$MD(A|E’) = \begin{cases} 1 & A的元素都出现在E’ \newline 0 & else \end{cases}$
$CER(H) = MD(A|E’) \times f(A)$
满足合取min，析取max

不确定的更新
$$
IF \quad THEN \quad H = \{ h_1,h_2,…,h_n \} \quad CF = \{ c_1,c_2,…,c_n \}
$$

求H的概率分配函数
- $m \{ \{h_1 \},\{ h_2 \},…,\} = (CER(E) \times c_1 ,…)$
- $m(\Omega) = 1 - \sum_{i=1}^n CER(E) \times c_i$
- 再正交，求f，CER
汉明距离：求两个模糊集之间的差异
- 离散：$d(F,G) = \frac{1}{n} \times \sum_{i=1}^n |\mu_F(u_i) - \mu_G(u_i)|$
- 连续：$d(F,G) = \frac{1}{b-a} \int_a^b |\mu_F(u_i) - \mu_G(u_i)| d(u)$
贴近度

$(F,G) = \frac{1}{2} \times (F \cdot G + (1 - F \bigodot G))$
- $F \cdot G = \vee_U (\mu_F(u_i) \wedge \mu_G(u_i))$
- $F \bigodot G = \wedge_U (\mu_F(u_i) \vee \mu_G(u_i))$

第六讲模糊推理方法

6.1 模糊逻辑提出

以经典集合为根基

6.2 模糊集合和隶属函数

论域：所讨论的全体对象，用$U$表示

元素：论域中每个对象，用$a,b,c,x,y,z$表示

集合：相同属性聚在一起的元素集

经典集合：集合中元素的关系只有两种，要么属于这个集合，要么不属于这个集合

模糊集合

给集合中每一个元素赋予一个介于0和1之间的实数，描述其属于一个集合的强度，该实数称为元素属于一个集合的隶属度。集合中所有元素的隶属度全体构成集合的隶属函数

表示方法：$A =${$(x,\mu_A(x)) , x \in X$} $\mu_A (x)$：元素$x$属于模糊集$A$的隶属度，$X$是元素$x$的论域

Zadeh表示法

1）数目有限

$A = \mu_A(x_1) / x_1 + \mu_A(x_2) / x_2 +…+\mu_A(x_n) / x_n = \sum_{i=1}^{n}{\mu_A(x_i) / x_i}$

$A=${$\mu_A(x_1) / x_1 ,\mu_A(x_2) / x_2 ,..,\mu_A(x_n) / x_n $}

2) 论域连续或元素无限

$A = \int_{x \in U} \mu_A(x)/x$

序偶表示法

$A =${$( \mu_A(x_1) , x_1) , ( \mu_A(x_2),x_2),…,( \mu_A(x_n) , x_n)$}

向量表示法

$A=${$\mu_A(x_1),\mu_A(x_2),…,(\mu_A(x_n),x_n),$}

隶属度

常见的隶属函数有正态分布、三角分布、梯形分布等

确定方法：模糊统计法、专家经验法、二元对比排序法、基本概念扩充法

6.3 模糊关系及其合成

模糊关系的构造

$R_m$：$\int_{U \times V} (\mu_F(u) \wedge \mu_G(v)) \vee (1-\mu_F(u)) / (u,v)$
$R_c$：$\int_{U \times V} (\mu_F(u) \wedge \mu_G(v)) / (u,v)$
$R_g$：$\mu_F(u) \rightarrow \mu_G(v) = \begin{cases} 1 & \mu_F(u) \leq \mu_G(v) \newline \mu_G(v) & \mu_F(u) > \mu_G(v)\end{cases}$

离散模糊集，用向量乘

$\mu_{A \times B} (a,b) = \mu_A^T \circ \mu_B $

上面的向量运算，把乘换成取小运算，加换成取大运算即可

6.4 模糊推理与模糊决策

模糊推理得到的就是模糊数

模糊决策：由模糊推理得到的结论或者操作是一个模糊向量，转化成为确定的过程

最大隶属度法：取最大的隶属度所对应的元素

加权平均判决法：$U = \frac{ \sum_{i=1}^{n} u (v_i) v_i}{\sum_{i=1}^n u (v_i)}$

中位数法：隶属度的中位数所对应的元素

6.5 模糊推理的应用

首先对于事实进行模糊合成$R$，然后在用条件$A’$与$R$合成$B’$，然后再进行模糊决策

第七讲搜索求解策略

7.1 搜索的概念

略

7.2 状态空间知识表示法

状态：表示系统状态、事实等叙述型知识的一组变量或数组$Q = [q_1,q_2,…,q_n]^T$
操作：表示引起状态变化的过程型知识的一组关系或函数$F =${$f_1,f_2,…,f_m$}
状态空间：利用状态变量和操作符号表示，四元组形式$(S,O,S_0,G)$
$S$：状态集合；$O$：操作算子的集合；$S_0$：包含问题的初始状态，为$S$的子集；$G$：若干具体状态或满足某些性质的路径信息描述。
求解路径：求$S_0$到$G$的路径
解：一个有限的操作算子序列$O_1O_2O_3…O_k$
$$
S_0\overset{O_1}{\rightarrow}S_1\overset{O_2}{\rightarrow}S_2\overset{O_3}{\rightarrow}…\overset{O_k}{\rightarrow}G
$$

7.3 启发式图搜索策略

启发式信息：用来简化搜索过程有关具体问题领域的特征的信息
启发式图搜索策略（利用启发信息的搜索方法）的特点：重排OPEN表，选择最有希望的节点加以扩展
- 每次更新策略函数，排序得到一个最优的策略进行更新操作
- 利用这种启发式信息的搜索过程称为启发式搜索
$A$算法、$A^*$算法

估价函数

估计节点的希望程度的量度
定义估价函数$f(n)$：从初始节点经过$n$到达目标节点的路径最小代价估计值
- $f(n) = g(n)+h(n)$
- $g(n)$：从初始节点$S_0$到节点$n$的实际代价
- $h(n)$：从节点$n$到目标节点的最优路径的估计代价，称为启发函数
- $h(n)$比重大：降低了搜索的工作量，但可能找不到最优解
- $h(n)$比重小：导致工作量加大，极限情况变为盲目搜索，一般都能找到最优解

$A$搜索算法

初始化
- OPEN表：待扩展节点
- CLOSED表：已扩展节点
每次寻找OPEN表中$f(n)$最小的点进行扩展，扩展完成之后加入CLOSED表

八数码问题

以下是一种启发搜索的策略

$g(n)$：节点$n$的深度

$h(n)$：节点$n$与目标棋局数位不相同的个数

$A^*$搜索算法

如果某一问题有解，那么利用$A^*$算法一定能找到最优解而结束

可采纳性：能找到解的搜索算法
单调性：$A^$中$h(n)$*单调不增**
信息性：如果$h_1(n) \leq h_2(n)$，称为$h_2$比$h_1$具有更多的信息性，如果$h(n)$越大，则信息性越多，所搜索状态就越少

第八讲遗传算法及其应用

位串编码

二进制编码
Gray编码（格雷码）
- 二进制串[$\beta_1\beta_2…\beta_n$]，Gray[$\gamma_1 \gamma_2 … \gamma_n$]
- $$
  \gamma_k =
  \begin{cases}
  \beta_1 & k=1
  \newline
  \beta_{k-1} \bigoplus \beta_k & k>1
  \end{cases}
  $$
- $$
  \beta_k = \sum_{i=1}^k \gamma_i(mod\ 2)
  $$

适应函数和尺度变换

线性变换：$f’ = af+b$
非线性变换
- 幂函数变换：$f’ = f^K$
- 指数变换：$f’ = e^{-af}$

选择

基本思想：适应度越高越容易被选择

在遗传算法中，关键就是个体的适应度和被选择个体的数目

适应度比例法或蒙特卡洛法
- $$
  p_{si} = \frac{f_i}{\sum_{i=1}^M f_i}
  $$
排序方法
- 线性排序
  - $x_1,x_2,…,x_N$
  - $$
    p_i = \frac{a-bi}{M(M+1)}
    $$
- 非线性排序
  - $$
    p_i =
    \begin{cases}
    q(1-q)^{i-1} & i=1,2,…,M-1
    \newline
    (1-q)^{M-1} & i=M
    \end{cases}
    $$

交叉

一($n$)点交叉：随机选择一($n$)点进行组合成新个体
部分匹配交叉：既要有新结构体出现，又要保证合法性

变异

位点变异：变换几个点
逆转变异：取出一段逆序再插入
等等

遗传算法的基本步骤

alt

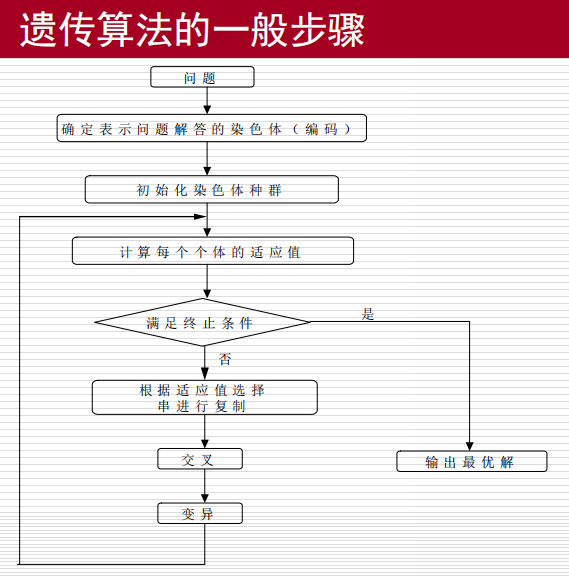
特点

全局优化概率算法

第九讲群智能算法及其应用

粒子群算法(PSO)

$$
v_j^i(k+1)=\omega(k)v_j^i(k)+\varphi_1 rand(0,a_1)(p_j^i(k)-x_j^i(k))+\varphi_2 rand(0,a_2)(p_j^g(k)-x_j^i(k))
$$

$P_j^i(k)$：$i$粒子走过最好的位置
$x_j^i(k)$：$i$粒子目前的位置
$p_j^g(k)$：群体走过最好的位置
$\varphi_1,\varphi_2$：控制个体认知分量和群体社会分量相对贡献的学习率的比重
$\varphi_1 > 0,\varphi_2>0$：PSO全模型
$\varphi_1 > 0,\varphi_2=0$：PSO认知模型
$\varphi_1 = 0,\varphi_2>0$：PSO社会模型
$\varphi_1 = 0,\varphi_2>0,g \neq i$：PSO无私模型

蚁群算法(ACO)

信息素跟踪、信息素遗留

BP神经网络

常用数学模型

线性激励模型
非线性激励模型
- $y = \begin{cases}
  1 & x\geq 0
  \newline
  0 & x<0
  \end{cases}$
- $y = \begin{cases}
  1 & x\geq 0
  \newline
  -1 & x<0
  \end{cases}$
- $y = \frac{1}{1+e^{- \alpha x}} \ \ \ \ \ \ \ \alpha = 1$
- $y = \frac{e^{\alpha x} - e^{- \alpha x}}{e^{\alpha x} + e^{- \alpha x}} \ \ \ \ \ \alpha = 1$

工作方式

神经网络结构
- 前馈型（前向型），前面一个神经元只影响后面的神经元
- 反馈型，后面的神经元可以影响到前面的神经元

BP神经网络

结构：输入层、输出层、隐层
Kolmogorov定理：给定任意$\varepsilon >0$，对于任意的$L_2$型连续函数$f:[0,1]^n \rightarrow R^m$，存在一个三层BP神经网络，其输入层有$n$个神经元，中间层有$2n+1$个神经元，输出层有$m$个神经元，它可以再任意$\varepsilon $平方误差精度内逼近$f$
目标函数：
- $$
  J = \frac{1}{2} \sum_{j=1}^{p_m}(y_j^m-d_j)^2
  $$
约束条件
- $$
  u_i^k = \sum_{j} w_{ij}^{k-1}y_j^{k-1} \ \ \ i=1,2,…,p_k
  $$
- $$
  y_i^k = f_k(u_i^k) \ \ \ k = 1,2,…,m
  $$
连接权值的修正量
- $$
  \Delta w_{ij}^{k-1} = - \varepsilon \frac{\partial J}{\partial w_{ij}^{k-1}} \ \ \ j=1,2,…,p_{k-1}
  $$
学习算法
- 正向传播：输入信息由输入层传至隐层，最终在输出层输出
- 反向传播：修改各层神经元的权值，使误差信号最小
BP算法设计
- 隐层数及隐层神经元的确定
- 初始权值设置，一般以一个均值为$0$的随机分布设置网络的初始权值
- 训练数据预处理：线性的特征比例变换，将所有的特征变换到[0,1]或者[-1,1]区间内，使得在每个训练集上，每个特征的均值为0，并且具有相同的方差
- 后处理过程
BP算法的实现
- 初始化：对于所有连接权和阈值赋值以随机任意小值$w_{ij}^k(t),\theta_i^k(t)(k=1,..,m;i=1,..,p_k;t=0)$
- 取出一组样本，输入
- 计算各层节点的输出$y_i^k$
- 计算误差：$e_i = y_i - y_i^m$
- 计算反向传播的误差
  - $$
    \Delta w_{ij} = -\alpha d_i^ky_j^{k-1}
    $$
  - $$
    d_i^m = y_i^m(1-y_i^m)(y_i^m-y_i)
    $$
  - $$
    d_i^k = y_i^k(1-y_i^k) \sum_{l=1}^{p_{k+1}}w_{li}^{k+1}d_l^{k+1}
    $$
- 重复上述过程，直到所有的误差满足条件
优点
- 很好的逼近特性
- 具有较强的泛化能力
- 具有较好的容错性
缺点
- 具有较好的容错性
- 局部极值
- 难以确定隐层和隐层结点的数目
应用
- 模式识别
- 软测量

Hopfield神经网络

离散型Hopfield

输入输出关系
- $x(k+1)=f(W_x(k) - \theta) , \forall i$
  - $X=[x_1,x_2,…,x_n]^T$
  - $\Theta=[\theta_1,\theta_2,..,\theta_n]^T$
  - $W=[w_{ij}] \ \ w_{ii}=0$
  - $F(s) = [f(s_1),f(s_2),…,f(s_n)]^T$
- $x_i(k+1) = f(\sum_{j=1}^n w_{ij}x_j(k) - \theta_i)$
- $f(x) = \begin{cases}
  1 & x\geq 0
  \newline
  -1 & x<0
  \end{cases}$
- $ f(x) = \begin{cases}
  1 & x\geq 0
  \newline
  0 & x<0
  \end{cases}$
工作方式
- 异步（串行）方式
  - $x_i(k+1) = f(\sum_{j=1}^n w_{ij}x_j(k) - \theta_i)$
  - $x_j(k+1) = x_j(k) \ \ \ j \neq i$
- 同步（并行）方式
  - $x(k+1)=f(W_x(k) - \theta) , \forall i$
  - $x_i(k+1) = f(\sum_{j=1}^n w_{ij}x_j(k) - \theta_i) \ \ \ \forall i$
通过给定的算法和由记忆样本的部分信息组成的初态，通过异步或者同步的方式（联想记忆）达到一个稳态（记忆样本）
稳态：从某一刻开始，网络中的神经元状态不再发生改变
稳定性定理
- 串行稳定性$W$：对称阵
- 并行稳定性$W$：非负定对称阵

连续性Hopfield

能量函数
- $$
  E = - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} w_{ij}v_iv_j - \sum_{i=1}^{n}v_iI_i+ \sum_{i=1}^{n} \frac{1}{R’} \int_{0}^{v_i}f^{-1}(v)dv
  $$
对于连续型Hopfield神经网络，若$f^{-1}(x)$为单调递增的连续函数，$C_i > 0 , w_{ij}=w_{ji}$，则$\frac{dE}{dt} \leq 0$；当且仅当$\frac{dv_i}{dt} = 0 , i \in [1,n]$时，$\frac{dE}{dt} = 0$

第一讲 人工智能概述