算法笔记
算法和过程
过程[程序] (Procedure)与算法 (Algorithm)是解决问题的一种方法的逐步描述:
相同点:由若干条指令组成的有穷序列;每条指令的意义都是确定的;具有零个或多个输入;产生若干个输出。
不同点:算法要求其执行时间是有限的(终止性),过程的执行时间可能是无限的
算法的复杂性取决于:求解问题的规模;具体的输入数据;算法本身的设计
时间复杂性$T(N,I)=\sum_{i=1}^{k}{t_i * e_i(N,I)}$
其中$t_i$为执行抽象计算机的第$i$种指令一次所需时间,这里假定抽象计算机共有$k$种指令。
$e_i(N,I)$为经过统计后得到的执行抽象计算机的第$i$种指令的次数。
常见符号及概念
上界记号$O$:如果存在整的常数$C$和自然数$N_0$,使得当$N \ge N_0$时有$f(N) \le C*g(N)$,则$f(N)$有上界函数$g(N)$,记为$f(N)=O(g(N))$。
下界记号$\Omega$:如果存在整的常数$C$和自然数$N_0$,使得当$N \ge N_0$时有$f(N) \ge C*g(N)$,则$f(N)$有下界函数$g(N)$,记为$f(N)=\Omega(g(N))$。
同阶记号$\Theta$:$f(N)=\Theta(g(N))$表示$f(N)$和$g(N)$同阶。
低阶记号$o$:$f(N) = o(g(N))$表示$f(N)$比$g(N)$阶低。
主方法求解递归式的时间复杂度
例:求$T(n) = 25*T(\frac{n}{5}) + n^2$,默认$T(1)=1$
- 主定理:设$a \geq 1 \ b>1$,设$f(n)$为一函数,$T(n) = a*T(\frac{n}{b}) + f(n)$,$\frac{n}{b}$向上取整或者向下取整对结果没有影响
- 若$f(n) < n^{log_b a}$:$T(n) = \Theta (n^{log_b a})$
- 若$f(n)=n^{log_b a}$: $T(n) = \Theta (n^{log_b a} logn)$
- 若$f(n) > n^{log_b a}$: $T(n) = \Theta (f(n))$
- 则上题为第二种情况:$T(n) = n^2 logn$
- 修改$T(n) = 25*T(\frac{n}{5}) + n^3$,则为第三种情况,$T(n)=n^3$
- 修改$T(n) = 25*T(\frac{n}{5}) + n^{1.5}$,则为第一种情况,$T(n)=n^2$
五种确定性算法,都使用递归的思想:
分支法,动态规划法(dp),贪心法,回溯法,分支界限法。
算法所具有的五大特性:有穷性,确定性、输入、输出、可行性
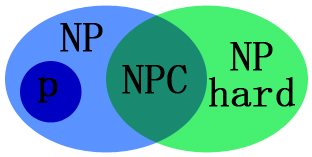
NP NPC P NP-Hard
- $P$类问题
- 有确定型图灵机在多项式时间内可解的一切判断问题的集合
- 能在多项式时间内解决的问题
- $NP$类问题
- 由非确定型图灵机在多项式时间内可解的判定问题的集合
- 不能在多项式时间内解决或不确定能不能在多项式时间内解决,但能在多项式时间验证的问题
- $NPC$类问题
- NP完全问题,所有在多项式时间内都能约化(Reducibility)到它的NP问题,即解决了此NPC问题,所有NP问题也都得到解决。
- $NP-Hard$类问题
- NP难问题,所有在多项式时间内都能约化(Reducibility)到它的问题(不一定是NP问题)。
密钥、私钥、公钥
- 密钥
- 在非对称加密技术中,有两种密钥,分为私钥和公钥,私钥是密钥对所有者持有,不可公布,公钥是密钥对持有者公布给他人的
- 公钥
- 公钥用来给数据加密,用公钥加密的数据只能使用私钥解密
- 私钥
- 用来解密公钥加密的数据
- 摘要
- 对需要传输的文本,做一个HASH计算,一般采用SHA1,SHA2来获得
- 签名
- 使用私钥对需要传输的文本的摘要进行加密,得到的密文即被称为该次传输过程的签名
- 签名验证
- 据接收端,拿到传输文本,但是需要确认该文本是否就是发送发出的内容,中途是否曾经被篡改。因此拿自己持有的公钥对签名进行解密(密钥对中的一种密钥加密的数据必定能使用另一种密钥解密。),得到了文本的摘要,然后使用与发送方同样的HASH算法计算摘要值,再与解密得到的摘要做对比,发现二者完全一致,则说明文本没有被篡改过

